Note su esercizi e verifiche di Goniometria
Verifiche del 28 Ottobre:
Alcuni chiarimenti:
-
La relazione tra arco di circonferenza $l$, il raggio $r$ e angolo sotteso $\alpha$
$$
l=\alpha \cdot r
$$
vale solamente per $\alpha$ espresso in radianti (infatti quella relazione viene proprio dalla definizione di angolo in radianti) e
non vale per angoli espressi in gradi. Si può ricavare anche una formula simile per gli angoli in gradi, basta aggiungere un coefficiente di conversione da gradi a radianti: $$ l=\alpha_{\text{gradi}} \cdot \frac{\pi}{180} \cdot r. $$ - Quando si usa la relazione $\cos^2 \alpha + \sin^2 \alpha =1$ per ricavare il coseno (o il seno) bisogna tenere presente il fatto che ci sono due possibili valori (uno positivo e uno negativo): $$\cos \alpha=\pm \sqrt{1-\sin^2\alpha}.$$ Di questi due valori eventualmente ne possiamo escludere uno nel caso in cui abbiamo altre informazioni sull'angolo $\alpha$ (ad esempio se sappiamo che $0<\alpha<\frac \pi 2$ escludiamo il valore negativo per il coseno e consideriamo solo quello positivo).
- Per dimostrare che una relazione come $$\sin^3\alpha=1-\cos(4\alpha)$$ non è valida per ogni $\alpha$ è sufficiente trovare un singolo angolo per cui la relazione ha senso (cioè si ottengono numeri a destra e a sinistra dell'uguale) ma l'uguaglianza risulta falsa. Nell'esempio possiamo provare con $\alpha=0$ ma otteniamo un'uguaglianza $0^3=1-1$, quindi non abbiamo dimostrato nulla. Possiamo quindi provare con $\alpha=\frac \pi 2$ e otteniamo $1^3=1-\cos(2\pi)=0$ che è falsa. Quindi possiamo concludere che la relazione non è valida per ogni $\alpha$.
Verifiche del 2 Dicembre:
Svolgimento di alcuni esercizi:
-
Perimetro di un ottagono regolare inscritto ad una circonferenza di raggio 1:
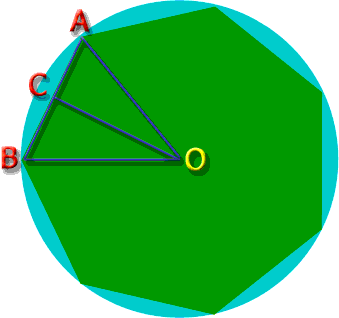
dal disegno si vede che il lato dell'ottagono inscritto è uguale al doppio del seno di un certo angolo. Per ricavare quell'angolo osserviamo che un ottagono è composto da 8 triangoli congruenti a quello rappresentato, e che quindi l'angolo al vertice centrale di ciascuno di essi deve essere l'ottava parte di un angolo giro: $\frac {2\pi}{8}=\frac {\pi}{4}$ (cioè $45^\circ$). Dunque la metà di quel triangolo (ciascuno dei triangoli rettangoli in figura) ha un angolo di $\frac \pi 8$. Il lato dell'ottagono è quindi $2\sin \frac \pi 8$. Tale valore si può ricavare con le formule di bisezione (\ref{bisezioneseno}): $$ \sin \frac \pi 8=+\sqrt{\frac{1-\cos\frac \pi 4}{2}}=\frac{\sqrt{2-\sqrt{2}}}{2} $$ e quindi il perimetro dell'ottagono è $8\times2\times\frac{\sqrt{2-\sqrt{2}}}{2}=6.1229...$ (nota che è vicino al valore $2\pi=6.2831...$, e il motivo dovrebbe essere evidente...)
-
Perimetro di un ottagono regolare circoscritto ad una circonferenza di raggio 1:
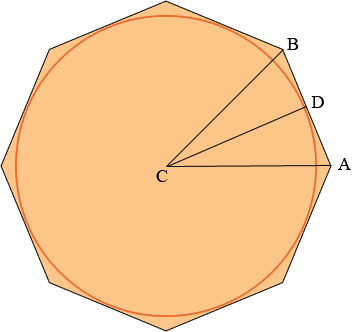
dal disegno si vede che il lato dell'ottagono circoscritto è uguale al doppio della tangente di un certo angolo. Per ricavare quell'angolo osserviamo (come nell'esercizio precedente) che un ottagono è composto da 8 triangoli congruenti a quello rappresentato, e che quindi l'angolo al vertice centrale di ciascuno di essi deve essere l'ottava parte di un angolo giro: $\frac {2\pi}{8}=\frac {\pi}{4}$ (cioè $45^\circ$). Dunque la metà di quel triangolo (ciascuno dei triangoli rettangoli in figura) ha un angolo di $\frac \pi 8$. Il lato dell'ottagono è quindi $2\tan \frac \pi 8$. Tale valore si può ricavare con le formule di bisezione (\ref{bisezionetangente}): $$ \tan \frac \pi 8=\frac{\sin \frac \pi 4}{1+\cos \frac \pi 4}=\sqrt{2}-1 $$ e quindi il perimetro dell'ottagono è $8\times2\times(\sqrt{2}-1)=6.6274...$ (anche stavolta è vicino al valore $2\pi=6.2831...$, per motivi altrettanto evidenti...)