Introduzione
Un tipico orologio digitale rappresenta il tempo con due numeri interi: il numero di ore (tra 0 e 23) trascorse dopo la mezzanotte e il numero di minuti (tra 0 e 60) trascorsi dall'inizio dell'ora corrente. Immaginiamo di poter rappresentare il tempo con la retta reale dove un numero reale indica il numero - non necessariamente intero - di secondi trascorsi da un certo istante iniziale. Rappresentiamo con un grafico il comportamento nel tempo dell'indicatore dei minuti dell'orologio digitale (ad esempio se è l'una e un quarto l'orologio indica $13:15$ e il numero di minuti indicati sarà $13$). Mettiamo quindi nell'asse $x$ il tempo effettivo in secondi e nell'asse $y$ il numero di minuti che indica l'orologio digitale. Chiamiamo $f(x)$ il numero di minuti che indica l'orologio al tempo $x$ (in secondi). Otteniamo un grafico di questo tipo:
Nota che il valore di $f(x)$ al variare di $x$ è stazionario su vari intervalli di tempo (ad esempio sull'intervallo che va da $0$ secondi a $60$ secondi, escludendo il valore $60$) e ha dei "salti" in corrispondenza degli estremi di questi intervalli di tempo: per $x< 60$ si ha $f(x)=0$ mentre per $x=60$ si ha $f(x)=1$. Se sappiamo che sono passati "circa $20$ secondi" possiamo ragionevolmente aspettarci che l'orologio segnerà $0$ minuti. Se invece sappiamo che sono passati "circa $60$ secondi" non siamo in grado di stabilire se l'orologio è su $0$ o su $1$ e questo a prescindere da quanto è grande l'incertezza del dato "circa $60$ secondi". Anche se sappiamo che sono passati $60 s$ con un'incertezza di $\pm 1/1000$ di secondo l'incertezza sui minuti segnati dall'orologio digitale rimane semmpre la stessa: una unità. Ad una incertezza sul valore di $x$ piccola quanto vogliamo corrisponde sempre una grande incertezza sul corrispondente valore $f(x)$ (più o meno $1$ minuto, nel nostro esempio) che non si riduce quando si riduce l'incertezza sul valore della $x$. Vediamo ora un esempio in cui questo non succede.
Consideriamo un orologio "analogico" a lancette e rappresentiamo con una funzione l'angolo che forma la lancetta dei minuti rispetto ad un' ipotetica retta orizzontale, al variare del tempo. Supponiamo di avere al tempo $0$ una lancetta dei minuti posizionata su $12$, cioè verticale, con angolo $\pi/2$. Il grafico dell'andamento dell'angolo (in radianti) al variare del tempo (sull'asse $x$) è il seguente:
Stavolta notiamo un andamento regolare e uniforme per tutti i valori $x$ del tempo. Se sappiamo che sono passati "circa $60$ secondi" possiamo dire che l'angolo sarà "circa $\frac \pi 2 + \frac{2\pi}{60}$". Dunque ad una piccola incertezza su un valore della $x$ corrisponde una piccola incertezza sul corrispondente valore $f(x)$.
Chiameremo "continue" le funzioni che si comportano come il secondo esempio: i valori di $f(x)$ hanno piccole variazioni in corrispondenza di piccole variazioni dei valori della $x$. Questo tipo di definizione è evidentemente vago e approssimativo e non è soddisfacente per impostare un discorso matematico rigoroso. Vediamo come può essere resa più precisa.
Definizione di continuità
Analizziamo la definizione che abbiamo esposto poco più sopra:
i valori di $f(x)$ hanno piccole variazioni in corrispondenza di piccole variazioni dei valori della $x$potremmo riformulare così:
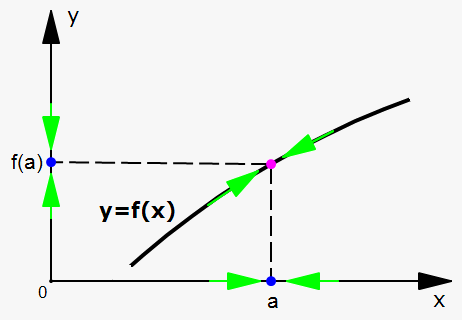
se $x$ è vicino a $x_0$ allora anche $f(x)$ è vicino a $f(x_0)$ma "vicino" è un termine ancora troppo vago e approssimativo, potremmo rendere il concetto meno vago riformulandolo così:
quanto più $x$ è vicino a $x_0$ tanto più anche $f(x)$ è vicino a $f(x_0)$questa formulazione somiglia molto al concetto di limite: stiamo affermando che "se $x$ tende a $x_0$ allora $f(x)$ tende a $f(x_0)$", in simboli: $$ \lim_{x\to x_0} f(x)=f(x_0). $$ Il concetto di limite è stato definito rigorosamente nella sezione precedente, quindi ora possiamo utilizzarlo per una definizione rigorosa di "funzione continua":
Diremo che $f(x)$ è continua nel punto $x_0$ se $\lim_{x\to x_0} f(x)=f(x_0)$.e inoltre
Diremo che $f(x)$ è continua sull'insieme $D$ se è continua in ogni punto $x_0\in D$.
Esempi e proprietà
Vediamo alcuni esempi di funzioni continue e alcune loro proprietà.
- La funzione $f(x)=x$ (nota anche come "funzione identità") è continua su tutto $\mathbb R$, questo deriva dal fatto (banale) che vale $\lim_{x\to x_0} x= x_0$, e dunque è soddisfatta la definizione sopra enunciata.
- Le funzioni costanti $f(x)=k$ (con $k$ che vale qualsiasi prefissato numero reale) sono continue su $\mathbb R$, questo deriva dal fatto banale che $\lim_{x\to x_0} k= k$.
Osserviamo che vale il seguente
Teorema 1:
Se $f(x)$ e $g(x)$ sono continue in $x_0$ allora sono continue in $x_0$ anche $f(x)+g(x)$, $f(x)\cdot g(x)$, e $f(x)^k$. Se vale anche $g(x_0)\neq 0$ è continua in $x_0$ anche la funzione $\frac{f(x)}{g(x)}$.
Infatti nella sezione sui limiti abbiamo visto che quando non ci troviamo di fronte a forme indeterminate il limite di una somma di due funzioni è uguale alla somma dei limiti, il limite di un prodotto è il prodotto dei limiti e il limite di un rapporto è il rapporto dei limiti. In questo caso è escluso che ci possano essere forme indeterminate perchè abbiamo $\lim_{x\to x_0} f(x)=f(x_0)$ (è la definizione di continuità) e quindi tale limite non può essere infinito. Lo stesso vale per $\lim_{x\to x_0} g(x)$, e nel caso del rapporto il teorema richiede anche che si abbia $g(x) \neq 0$, che è sufficiente ad escludere tutte le forme indeterminate. Per $f(x)^k$ è sufficiente applicare il teorema ripetutamente ai prodotti $f(x)\cdot f(x)$, $f(x)^2 \cdot f(x)$, eccetera fino a ottenere la continuità di $f(x)^k$.
Grazie al suddetto teorema è possibile costruire molti altri esempi di funzioni continue:
- Le funzioni che hanno la forma $f(x)=mx+q$ (cioè quelle che rappresentano delle rette in forma esplicita) sono continue su $\mathbb R$, questo discende dai due esempi precedenti e dall'applicazione del teorema 1 al prodotto $m\cdot x$ e alla somma $mx+q$.
- Le funzioni polinomiali $f(x)=P(x)$, dove $P(x)$ è appunto un polinomio, sono continue su tutto $\mathbb R$. Questo discende dagli esempi precedenti e dall'applicazione reiterata del teorema 1 a $x^k$ e alle somme dei termini che compongono il polinomio.
- L'iperbole $f(x)=\frac 1 x$ è continua su tutto il suo dominio, quindi per $x \in \mathbb R$ con $x \neq 0$. Questo discende dal teorema 1 considerando il rapporto tra la funzione continua $f(x)=1$ (costante) e la funzione continua $g(x)=x$ (identità), il teorema sarà applicabile per $g(x)\neq 0$ ovvero $x\neq 0$.
- Le funzioni razionali $f(x)=\frac {P(x)} {Q(x)}$, dove $P(x)$ e $Q(x)$ sono polinomi, sono continue su tutto il loro dominio, quindi per $x \in \mathbb R$ con $Q(x) \neq 0$. Questo discende dal teorema 1 il rapporto tra la funzione continua $f(x)=P(x)$ (polinomiale) e la funzione continua $g(x)=Q(x)$ (polinomiale), il teorema sarà applicabile per $g(x)\neq 0$ ovvero $Q(x)\neq 0$.
- La funzione esponenziale $f(x)=A^x$ con $A>0$ è continua su tutto $\mathbb R$.
- La funzione logaritmo $\log_b(x)$ è continua sul suo dominio $D=\{x>0\}$.
- Le radici $n$-esime $f(x)=\sqrt[n]{x}$ sono continue sul loro dominio, quindi per $n$ dispari sono continue su tutto $\mathbb R$, per $n$ pari sono continue su $D=\{x\geq 0\}$.
Chiaramente è possibile combinare le funzioni fino ad ora elencate con somme, prodotti e rapporti generando altre funzioni che saranno a loro volta continue grazie al teorema 1. Ma si può fare molto di più razie ad un altro teorema:
Teorema 2:
Se $f(x)$ è continua in $x_0$ e $g(x)$ è continua in $f(x_0)$ allora la funzione composta $g(f(x))$ è continua in $x_0$.