Introduzione
Sappiamo che è possibile definire una funzione $f: A \to B$ considerando un
Definizione
Date due funzioni $f:A \to B$ e $g: B \to C$ definiamo la "composizione" di $f$ con $g$ nel seguente modo:
Seno e coseno di angoli particolari
Link
Relazioni tra seno, coseno e cateti di un triangolo rettangolo
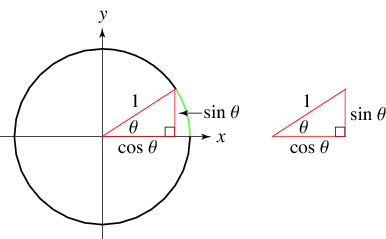
Sulla circonferenza goniometrica si può individuare il seguente triangolo rettangolo di ipotenusa pari ad $1$:
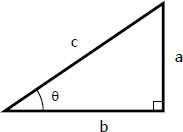
questo trangolo sarà simile ad un triangolo rettangolo con lo stesso angolo al vertice (l'altro dovrà coincidere perchè la somma deve dare sempre un angolo piatto) ma con un'ipotenusa differente, come questo:
Dalle proprietà dei triangoli simili possiamo dedurre che valgono le seguenti relazioni (con riferimento ai due triangoli rappresentati qui sopra):
$$\frac c 1 = \frac a {\sin \theta } = \frac b {\cos \theta }$$
e quindi:\[\begin{aligned} a=c\cdot \sin\theta, \end{aligned} \]
\[\begin{aligned} b=c\cdot \cos\theta. \end{aligned} \]
Formule per la somma di angoli
\begin{equation}\label{senosomma} \sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta) \end{equation}
\begin{equation}\label{cosenosomma} \cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) \end{equation}
Dimostrazione:
Per ricavare alcune delle lunghezze indicate nella figura è necessario usare le formule viste sopra per il generico triangolo rettangolo: $a=c\cdot \sin(\theta)$ e $b=c\cdot \cos(\theta)$, dove consideriamo $\theta=\alpha$, in un caso $c=\sin(\beta)$ e in un altro $c=\cos(\beta)$.
Possiamo usare le formule precedenti per ricavare la tangente di una somma di due angoli:
\begin{equation}\label{tangentesomma} \begin{aligned} & \tan(\alpha+\beta) = \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\ & = \frac {\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)}{\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)} \\ & = \frac {\frac{\sin(\alpha)\cos(\beta)}{\cos(\alpha)\cos(\beta)}+\frac{\cos(\alpha)\sin(\beta)}{\cos(\alpha)\cos(\beta)}}{\frac{\cos(\alpha)\cos(\beta)}{\cos(\alpha)\cos(\beta)}-\frac{\sin(\alpha)\sin(\beta)}{\cos(\alpha)\cos(\beta)}} \\ & = \frac {\frac{\sin(\alpha)}{\cos(\alpha)}+\frac{\sin(\beta)}{\cos(\beta)}}{1-\frac{\sin(\alpha)}{\cos(\alpha)}\frac{\sin(\beta)}{\cos(\beta)}} \\ & = \frac {\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)} \end{aligned} \end{equation}
Parità e disparità
Per tutti gli angoli valgono le seguenti uguaglianze verificabili facilmente per via geometrica sulla circonferenza:
\begin{equation}\label{senodispari} \sin(-\alpha)=-\sin(\alpha) \end{equation}
\begin{equation}\label{cosenopari} \cos(-\alpha)=\cos(\alpha) \end{equation}
\begin{equation}\label{tangentedispari} \begin{aligned} \tan(-\alpha) & =\frac{\sin (-\alpha)}{\cos(- \alpha)}\\ &=\frac{-\sin \alpha}{\cos \alpha}=-\tan \alpha \end{aligned} \end{equation}
Differenza di angoli
Dalle formule della somma (\ref{senosomma}) e (\ref{cosenosomma}) si possono ricavare le formule per la differenza semplicemente sommando gli angoli $\alpha$ e $-\beta$ e utilizzando le formule di parità/disparità (\ref{senodispari}) e (\ref{cosenopari}). Si ottiene:
\[\begin{aligned} \sin(\alpha-\beta) & = \sin(\alpha+(-\beta))\\ & = \sin(\alpha)\cos(-\beta)+\cos(\alpha)\sin(-\beta) \\ & = \sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta) \end{aligned} \]
\[\begin{aligned} \cos(\alpha-\beta) & = \cos(\alpha+(-\beta))\\ & = \cos(\alpha)\cos(-\beta)-\sin(\alpha)\sin(-\beta) \\ & = \cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta) \end{aligned} \]
Per la tangente della differenza usiamo insieme la formula della somma (\ref{tangentesomma}) e la formula della disparità (\ref{tangentedispari}) e otteniamo:
\begin{equation*} \begin{aligned} \tan(\alpha-\beta) & = \tan(\alpha+(-\beta))\\ & = \frac {\tan(\alpha)+\tan(-\beta)}{1-\tan(\alpha)\tan(-\beta)} \\ & = \frac {\tan(\alpha)-\tan(\beta)}{1+\tan(\alpha)\tan(\beta)} \end{aligned} \end{equation*}Formule di duplicazione
Le formule di bisezione permettono di esprimere seno, coseno e tangente del doppio di un angolo ($2 \alpha$) sfruttando informazioni relative all'angolo di partenza ($\alpha$).
Per ricavare le formule di duplicazione è sufficiente considerare le formule per la somma di angoli ($\ref{senosomma}$) e ($\ref{cosenosomma}$) per sommare due volte lo stesso angolo: \begin{equation}\label{duplicazioneseno} \sin(2\alpha)=\sin(\alpha+\alpha)=2\sin\alpha\cos \alpha \end{equation} \begin{equation}\label{duplicazioncoeseno} \cos(2\alpha)=\cos(\alpha+\alpha)=\cos^2 \alpha-\sin^2\alpha. \end{equation}
Formule di bisezione
Le formule di bisezione permettono di esprimere seno, coseno e tangente della metà di un angolo ($\frac \alpha 2$) sfruttando informazioni relative all'angolo intero ($\alpha$).
Per ricavare le formule di bisezione partiamo dalla formula di duplicazione del coseno: $ \cos(2\beta)=\cos^2(\beta)-\sin^2(\beta) $ e poniamo $\beta=\frac \alpha 2$ (e quindi $2\beta=\alpha$). Otteniamo $$ \cos(\alpha)=\cos^2\left(\frac \alpha 2\right)-\sin^2\left(\frac \alpha 2\right). $$ Da questa formula e dalla relazione fondamentale ($\ref{fondamentale}$) si ricavano le formule \begin{equation}\label{bisezionecoseno} \cos^2\left(\frac\alpha 2\right)=\frac{1+\cos \alpha}{2} \end{equation} \begin{equation}\label{bisezioneseno} \sin^2\left(\frac \alpha 2\right)=\frac{1-\cos \alpha}{2} \end{equation}
Per la tangente partiamo dalla relazione $$ \tan\left(\frac \alpha 2\right)=\frac{\sin\left(\frac \alpha 2\right)}{ \cos\left(\frac \alpha 2\right)} $$ e moltiplichiamo numeratore e denominatore per $\sin\left(\frac \alpha 2\right)$. Otteniamo: $$ \tan\left(\frac \alpha 2\right)=\frac{\sin^2\left(\frac \alpha 2\right)}{ \sin\left(\frac \alpha 2\right) \cos\left(\frac \alpha 2\right)} $$ poi osserviamo che possiamo applicare (\ref{bisezioneseno}) al numeratore, mentre per il denominatore sfruttiamo la formula: $$ \sin(\alpha)=2\sin\left(\frac \alpha 2\right) \cos\left(\frac \alpha 2\right) $$ ottenuta applicando la formula di duplicazione (\ref{duplicazioneseno}) all'angolo $\beta=\alpha/2$. Sostituendo le espressioni delle formule citate a numeratore e denominatore di $\tan(\alpha/2)$ (e semplificando i $2$ che compaiono a numeratore e denominatore) si ottiene: $$ \tan\left(\frac \alpha 2\right)=\frac{1-\cos(\alpha)}{ \sin(\alpha)} $$ Notiamo che sempre a partire da $\tan\left(\frac \alpha 2\right)=\frac{\sin\left(\alpha /2\right)}{ \cos\left(\alpha/ 2\right)}$ potevamo moltiplicare numeratore e denominatore per $\cos\left(\alpha /2\right)$ e ragionare come sopra sfruttando (\ref{bisezionecoseno}) anzichè (\ref{bisezioneseno}). Alla fine si arriva ad una formula simile a quella ricavata sopra: \begin{equation}\label{bisezionetangente} \tan\left(\frac \alpha 2\right)=\frac{ \sin(\alpha)}{1+\cos(\alpha)} \end{equation}